Heat kernel approximations

This page includes two methods to approximate the heat kernel. Both methods are wrapped in HeatFilter. By default we use the Chebyshev polynomials, but we can also use the Backward Euler methods with Cholesky decomposition.

The important parameters of HeatFilter are

• The order of polynomials degree (or discretization steps if using Euler), by default we use order=32 (the same as pygsp).

• The diffusion time tau.

In practice, we one can try a smaller order as it can make the algorithm faster, while maintaining good accuracy.

Diffusion of Dirac on a path graph

Note

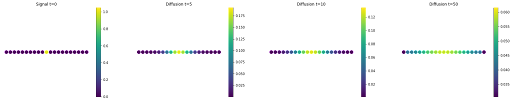
The backward Euler approximation could be made faster with scikit_sparse, but we currently have dependencies issues with this packages.

---

source

HeatFilter

 HeatFilter (graph:Any, tau:float, order:int, method:str)

Wrapper for the approximation of the heat kernel.

	Type	Details
graph	Any	Graph object
tau	float	Diffusion time
order	int	Degree or numver of steps
method	str	filter "pygsp", "mar", "euler"
Returns	Callable

---

source

HeatEuler

 HeatEuler (L, t, K)

Implicit Euler discretization of the heat equation using Cholesky prefactorization.